Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 코딩테스트 준비
- 99클럽
- 배열
- github
- Java
- 코딩
- CS
- Entity
- GIT
- 개발자 취업
- 면접(java
- HTML
- ArrayList
- 정렬 알고리즘(sort algorithm)
- 항해99
- 이진 탐색(binary search)
- css
- 코딩공부
- 메서드
- 자바
- 자료구조
- Til
- Spring
- 프로그래머스
- 코딩문제
- cs 공부)준비
- aop
- wil
- 회고
- Grafana
Archives
- Today
- Total
hayu's 개발 일지
99클럽 코테 스터디 34일차 TIL + Big-O 표기법(2) 본문

학습 키워드
-
공부한 내용
빅오 복잡성 차트(Big-O Complexity Chart)
💡 빅오 표기법을 이용하여 알고리즘의 시간 복잡도를 분석하면, 입력 크기가 커질 때 어떤 알고리즘이 더 효율적인지 비교할 수 있다.

https://www.bigocheatsheet.com/
표기법 이름 시간 복잡도 설명 예시
| O(1) | 상수 | 상수 시간 | 입력 크기와 상관없이 일정한 실행 시간을 가집니다. | 배열에서 원소 하나 찾기 |
| O(logn) | 로그 | 로그 시간 | 입력 크기가 증가함에 따라 실행 시간이 로그함수의 형태로 증가합니다. | 이진 탐색 알고리즘 |
| O(n) | 선형 | 선형 시간 | 입력 크기와 비례하는 실행 시간을 가집니다. | 선형 탐색 알고리즘 |
| O(nlogn) | 로그 선형 | 선형 로그 시간 | 입력 크기가 증가함에 따라 실행 시간이 로그함수와 선형 함수의 곱의 형태로 증가합니다. | 병합 정렬, 힙 정렬 알고리즘 |
| O(n^2) | 이차 | 이차 시간 | 입력 크기의 제곱에 비례하는 실행 시간을 가집니다. | 선택 정렬, 버블 정렬, 퀵 정렬 알고리즘 |
| O(2^n) | 지수 | 지수 시간 | 입력 크기의 지수에 비례하는 실행 시간을 가집니다. | 부분집합 |
| O(n!) | 계승 | 팩토리얼 시간 | 입력 크기의 팩토리얼에 비례하는 실행 시간을 가집니다. | 외판원 문제 |
표기법 예시
O(1): 상수 시간 알고리즘
- 입력 데이터와 상관없이 일정하게 증가하는 알고리즘, 시간과 요소와 일정하게 증가한다.
- 위에 그래프를 참조해봐도 O(log n) , O(1)은 입력 데이터와 상관없이 시간이 따로 늘어나지 않음을 확인할 수 있다.
- stack에서의 Push, Pop
- 배열에서 원소 하나를 찾는 예시이다.
// O(1)public static int getFirst(int[] nums) {
return nums[0];
}
O(log n): 로그 시간 알고리즘
- 대표적인 알고리즘으로는 이진 검색법이다. (binary search)
- 그래프를 참조하여보면 O(n) 보다도 O(log n)에 시간은 적다.
- 데이터가 증가하더라도, 시간이 크게 증가하지 않는다.
- 이진 검
- 이진 탐색 알고리즘의 예시이다.
// O(log n)public static int binarySearch(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
O(n) : 선형 시간 알고리즘
- 입력 데이터의 크기에 비례하여 입력시간도 같은 비율로 늘어나는 알고리즘이다.
- 선형 검색(2개 이상의 복잡도로 구성된 알고리즘의 전체 복잡도는 차원이 더 높은 쪽의 복잡도를 우선시한다.)
- for문
- 해당 코드는 입력한 배열을 역순으로 만드는 함수를 구현한 예시이다.
// O(n)public static int[] reverse(int[] nums) {
int[] reversed = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
reversed[nums.length - i - 1] = nums[i];
}
return reversed;
}
O(n log n): 로그 선형 알고리즘
- 퀵 정렬, 병합정렬, 힙 정렬
- 해당 코드는 병합 정렬(merge sort)을 이용해 정렬하는 예시이다.
// O(n log n)public static void mergeSort(int[] nums, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
}
O(n^2): 이차 시간 알고리즘
- 입력 데이터 받은 n만큼 루프를 돌리는데, 그 안에서 루프를 또 n만큼 돌리게 될 때의 표기방법이다.
- n에 요소 하나당 n 만큼씩 늘어남으로 작은 양의 데이터일 땐 문제가 없지만 많아지면 많아질수록 위에 그래프와 같이 한 번에 수직 상승한다.
- 입력값 n이 크다고 가정했기 때문에, 3n, 5n을 O(n)으로 표기하는 것 처럼, n^3과 n^5도 O(n^2)라고 표기한다.
- 이중 for문, 삽입정렬, 거품정렬, 선택정렬
- 해당 코드는 정수 배열을 선택 정렬(selection sort)을 이용해 정렬하는 예시이다.
// O(n^2)public static void selectionSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
int minIdx = i;
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] < nums[minIdx]) {
minIdx = j;
}
}
int tmp = nums[i];
nums[i] = nums[minIdx];
nums[minIdx] = tmp;
}
}
O(2^n):지수 시간 알고리즘
- 재귀로 구현하는 fibonacci 수열
- 해당 코드는 피보나치수열을 구하는 예시이다.
// O(2^n)public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
정렬 알고리즘으로 바라본 시간/공간 복잡도
시간 복잡도 관점
- 시간 복잡도 관점에서는 ‘입력된 값’을 기반으로 ‘수행시간’에 따라서 나뉜다.
- 일반적으로 알고리즘을 선택할 때는 최악의 경우를 보는 것이 좋다.
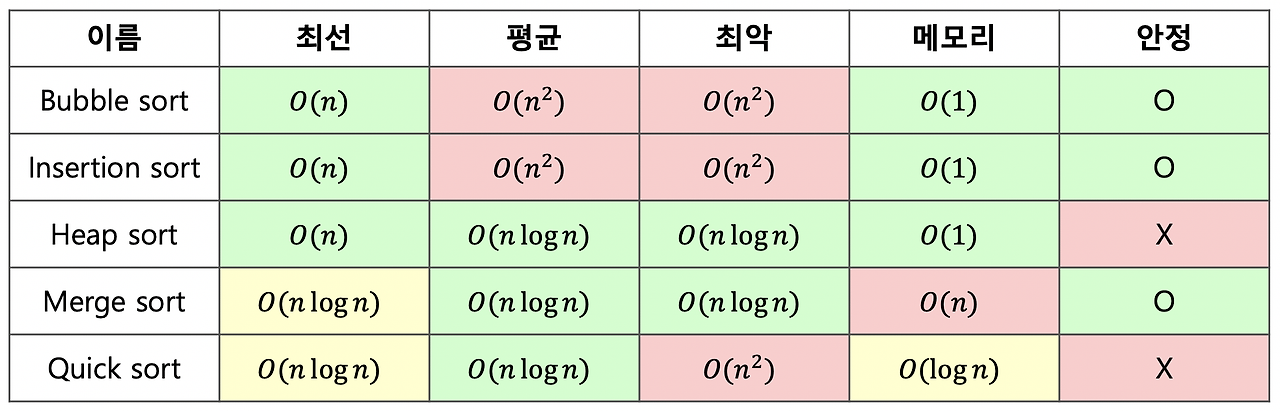
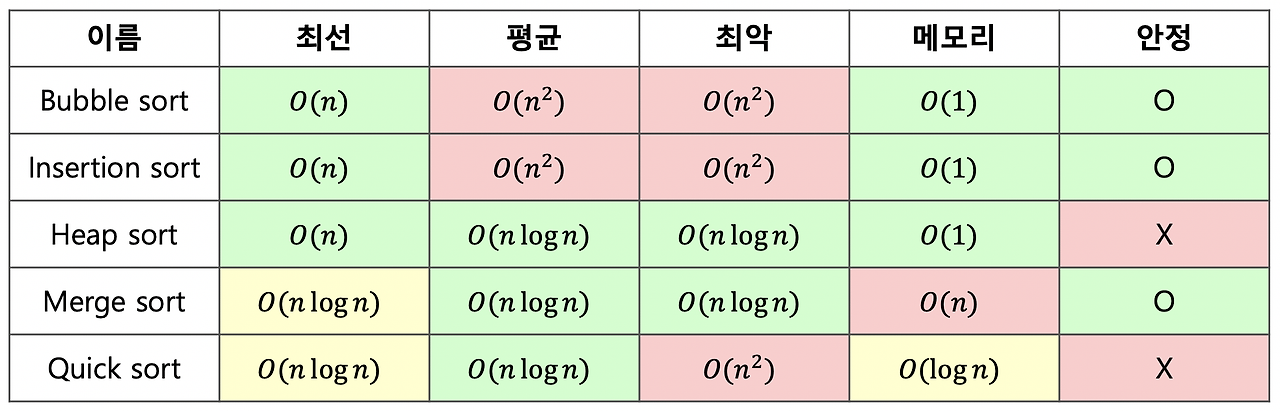
공간 복잡도 관점
- 공간 복잡도 관점에서는 시간 복잡도와 함께 ‘메모리 공간의 양’에 따라서 나뉜다.
참고 자료
'자료구조&알고리즘' 카테고리의 다른 글
| 99클럽 코테 스터디 37일차 TIL + 이진 탐색(Binary Search)(2) (0) | 2024.06.26 |
|---|---|
| 99클럽 코테 스터디 36일차 TIL + 이진 탐색(Binary Search)(1) (0) | 2024.06.25 |
| 99클럽 코테 스터디 33일차 TIL + Big-O 표기법(1) (0) | 2024.06.22 |
| 99클럽 코테 스터디 32일차 TIL + 우선순위 큐(PriorityQueue)(2) (0) | 2024.06.21 |
| 99클럽 코테 스터디 31일차 TIL + 우선순위 큐(PriorityQueue)(1) (0) | 2024.06.20 |




